TABLAS FUNCIONALES Y FUNCIÓN BOOLEANA

Función booleana

En matemáticas, una función booleana es una función cuyo dominio son las palabras conformadas por los valores binarios 0 ó 1 ("falso" o "verdadero", respectivamente), y cuyo codominio son ambos valores 0 y 1.

Formalmente, son las funciones de la forma ƒ : Bⁿ → B, donde B = {0,1} y n un entero no negativo correspondiente a la aridad de la función.

Modos de representación

Existen distintas formas de representar una función lógica, entre las que podemos destacar las siguientes:

·         Algebraica

·         Por tabla de verdad

·         Numérica

·         Gráfica

El uso de una u otra, como veremos, dependerá de las necesidades concretas en cada caso.

Algebraica

Se utiliza cuando se realizan operaciones algebraicas. A continuación se ofrece un ejemplo con distintas formas en las que se puede expresar algebraicamente una misma función de tres variables.

a) F = [(A + BC’)’ + ABC]’ + AB’C

b) F = A’BC’ + AB’C’ + AB’C + ABC’

c) F = (A + B + C)(A + B + C’)(A + B’ + C’)(A’ + B’ + C’)

d) F = BC’ + AB’

e) F = (A + B)(B’ + C’)

f) F = [(BC’)’(CB)´ (AB’)’]’

g) F = [(A + B)’ + (B’ + C’)’]’

La expresión a) puede proceder de un problema lógico planteado o del paso de unas especificaciones a lenguaje algebraico. Las formas b) y c) reciben el nombre expresiones canónicas: de suma de productos (sum-of-products, SOP, en inglés), la b), y de productos de sumas (product-of-sums, POS, en inglés), la c); su característica principal es la aparición de cada una de las variables (A, B y C) en cada uno de los sumandos o productos.

Por tabla de verdad

Una tabla de verdad contiene todos los valores posibles de una función lógica dependiendo del valor de sus variables. El número de combinaciones posibles para una función de n variables vendrá dado por 2ⁿ. Una función lógica puede representarse algebraicamente de distintas formas como acabamos de ver, pero sólo tiene una tabla de verdad. La siguiente tabla corresponde a la función lógica del punto anterior.

La forma más cómoda para ver la equivalencia entre una tabla de verdad y una expresión algebraica es cuando esta última se da en su forma canónica. Así, la función canónica de suma de productos (o forma canónica disyuntiva)

F = A’BC’ + AB’C’ + AB’C + ABC’

nos indica que será 1 cuando lo sea uno de sus sumandos, lo que significa que tendrá por lo tanto cuatro combinaciones que lo serán (010 para A’BC’, 100 para AB’C’, 101 para AB’C y 110 para ABC’) siendo el resto de combinaciones 0. Con la función canónica de producto de sumas (o forma canónica conjuntiva) se puede razonar de forma análoga, pero en este caso observando que la función será 0 cuando lo sea uno de sus productos.

También es fácil obtener la tabla de verdad a partir de la función simplificada, pero no así a la inversa.

Numérica

La representación numérica es una forma simplificada de representar las expresiones canónicas. Si consideramos el criterio de sustituir una variable sin negar por un 1 y una negada por un 0, podremos representar el término, ya sea una suma o un producto, por un número decimal equivalente al valor binario de la combinación. Por ejemplo, los siguientes términos canónicos se representarán del siguiente modo (observe que se toma el orden de A a D como de mayor a menor peso):

AB’CD = 1011₂ = 11₁₀

A’ + B + C’ + D’ = 0100₂ = 4₁₀

Para representar una función canónica en suma de productos utilizaremos el símbolo Σ_n (sigma) y en producto de sumas Π_n (pi), donde n indicará el número de variables. Así, la representación numérica correspondiente a la tabla de verdad del punto anterior quedará como:

F = Σ₃(2, 4, 5, 6) = Π₃(0, 1, 3, 7)

Matemáticamente se demuestra, que para todo término i de una función, se cumple la siguiente ecuación:

F = [Σ_n(i)]' = Π_n(2ⁿ-1-i )

A modo de ejemplo se puede utilizar esta igualdad para obtener el producto de sumas a partir de la suma de productos del ejemplo anterior:

F = Σ₃(2, 4, 5, 6) = [Σ₃(2, 4, 5, 6)]' ' = [Σ₃(0, 1, 3, 7)]' = Π₃(0, 1, 3, 7)

Gráfica

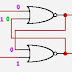
La representación gráfica es la que se utiliza en circuitos y esquemas electrónicos. En la siguiente figura se representan gráficamente dos funciones algebraicas, una con símbolos no normalizados, superior, y la otra con normalizados, inferior (véanse los símbolos de las puertas lógicas)

Representación gráfica de dos funciones lógicas

1.      Tablas De Verdad

Son un medio para describir la manera en que la salida de un circuito lógico depende de los niveles lógicos que haya en la entrada del circuito.
En una tabla se muestra que ocurre al estado de salida con cualquier grupo de condiciones de entrada, los verdaderos valores de salida dependerán del tipo de circuito lógico.
El número de combinaciones de entrada será igual a 2 para una tabla de verdad con "n" entradas.

Dos de los teoremas más importantes del álgebra booleana fueron enunciados por el matemático DeMorgan. Los Teoremas de DeMorgan son de gran utilidad en la simplificación de expresiones en las cuales se invierte un producto o suma de variables. Los dos teoremas son:

a) La expresión booleana es:

 F (A, B, C, D)=

aplicando las leyes de DEMORGAN

F (A, B, C, D)=
F (A, B, C, D)=

Como tenemos 4 entradas entonces para la tabla sería: 2 , entonces tenemos 16 combinaciones.

A	B	C	D	F
0	0	0	0	1
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	1
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	1
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

b) La expresión booleana es:

 F (A, B, C, D)=

Como tenemos 4 entradas entonces para la tabla sería: 2 , entonces tenemos 16 combinaciones.

A	B	C	D	F
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	0
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

c) La expresión booleana es:

 F (A, B, C, D)=

Como tenemos 4 entradas entonces para la tabla sería: 2 , entonces tenemos 16 combinaciones.

A	B	C	D	F
0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	0
0	1	1	1	0
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	0
1	1	0	0	0
1	1	0	1	1
1	1	1	0	1
1	1	1	1	1

2.      Escribir la expresión booleana y la tabla de verdad de los circuitos mostrados

Dibujar un diagrama de circuito lógico, utilizando solo compuertas NAND de 2 entradas.
Asumir que solo disponemos de entradas directas(sin complementar)
Utilice 7400 y numere los pines para todas las conexiones en su circuito.

La fórmula se pueda escribir como:

Siguiendo la ley de DEMORGAN

X	Y	Z	F
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 1 1 1 0 1 0 0

3.      Escribir la tabla de verdad para la función lógica:

a) XOR de 2 entradas

A	B	Z
0	0	0
0	1	1
1	0	1
1	1	0

A	B	C	Z
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 1 1 0 1 0 0 1

b) XOR de 3 entradas

4.      Dibujar la tabla de verdad y la expresión booleana e una puerta XOR de 2 y 3 entradas.

A	B	C	F
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	1 1 1 0 1 0 1 0

5.      Escriba la tabla de verdad de la función: F = ((A + B). C)

La expresión Booleana:

Z =

A	B	Z
0	0	0
0	1	1
1	0	1
1	1	0

6.      Escribir la expresión booleana y la tabla de verdad del circuito mostrado:

C	B	A	Y
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 1 0 0 1 0 0 0

7.      Diseñar el circuito que responde a la siguiente tabla de verdad

8.      Obtener la función booleana el siguiente circuito. Implementar con CI-TTL simplificar el circuito y verificar la equivalencia.

La función booleana es la siguiente:

X	Y	Z	F
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 1 1 1 0 1

Simplificando:

El circuito es el siguiente:

X	Y	Z	F
0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1	0 0 0 1 1 1 0 1