TABLAS DE BIESTABLES

Tabla de Funcionamiento

Los fabricantes de circuitos integrados, para describir la operación que realiza el circuito, emplean la llamada tabla de funcionamiento, que es lo que hasta ahora hemos venido llamando tabla de verdad para los circuitos combinacionales, a la que se ha añadido el estado del tiempo, que resulta esencial para los circuitos secuenciales.

La tabla de funcionamiento del biestable S-R, resulta ser:

Hemos empleado la siguiente notación:

t_n = instante de tiempo en el que se aplican las entradas.

t_n+1 = instante de tiempo inmediatamente posterior en el que el circuito responde.

Q₀ = salida Q en el instante t_n

Q+ = salida en el instante t_n+1

Aunque el flip-flop SR tiene dos entradas S y R, y una salida Q, es habitual que al implementarlo aparezca con otra salida más, la resultante de complementar la salida Q, y la entrada de reloj C.

Se suele representar simbólicamente como un rectángulo como se indica en la figura.

Imagen 01. elaboración propia

 

Diseño de un biestable S-R (Set- Reset)

Estos circuitos se pueden diseñar siguiendo las técnicas que hemos venido empleando en el diseño de los circuitos combinacionales, sin más que tener en cuenta, que los circuitos secuenciales presentan una realimentación.

Vamos a aplicar el método al diseño de un flip-flop S-R. En nuestro caso la salida Q+ depende tanto de la salida anterior Q₀, como de las entradas S y R, por lo que para implementarlo vamos a tratarlo como a un circuito combinacional, pero considerando que Q₀ es también una entrada, por lo que manejaremos la tabla de verdad que se adjunta, a partir de la tabla de estado que acabamos de comentar.

Las entradas a cero no producen variación del valor de salida.

Si la entrada S es 1, el valor de la salida pasa a 1.

Si la entrada R es 1, el valor de la salida pasa a 0.

Las dos entradas a uno (no se utilizan) dan una salida indeterminada.

Que al simplificar quedará:

Aunque no es el procedimiento habitual, se consigue una función más simplificada si despreciamos los términos indiferentes del mapa de Karnaugh. Por lo tanto se hacen dos bolsas de dos celdas y se obtiene:

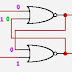
Si lo implementamos empleando únicamente puertas NOR:

Que una vez implementado quedará

Imagen 02. Elaboración propia

Esta implementación tiene la ventaja de que también produce la función en la salida de la primera puerta NOR, de modo que se suele dibujar este circuito (en el circuito y en muchas ocasiones, :

Imagen 03. Elaboración propia

En el caso de un biestable R-S síncrono por nivel alto sería:

Imagen 04. elaboración propia	Imagen 05. elaboración propia

Su cronograma y su tabla de estados sería:

 

Imagen 06. Elaboración propia

Se conocen por el nombre de biestables de datos o seguidores. Tienen una única entrada D, que es copiada en el interior del biestable en los instantes de sincronismo.

Solamente tienen sentido como biestables síncronos por nivel o por flanco.

Su tabla de funcionamiento será:

El nuevo estado Q_t+1 es 1. si D está activa 1 en el instante de sincronismo.
El nuevo estado Q_t+1 es 0, si D está inactiva 0 en el instante de sincronismo

Vamos a considerar que la entrada D es activa por nivel alto, con lo que su circuito será

Imagen 07. Elaboración propia

Su símbolo

Imagen 08. Elaboración propia

y su tabla de estados sería;

Por tanto, su función lógica sería

Su funcionamiento es similar al flip-flop R-S, de modo que la entrada K actúa para la puesta a 0 (reset) y la entrada J para la puesta a 1 (set). Cuando se activan las dos entradas simultáneamente, el biestable cambia de estado. Son biestables síncronos, lo que quiere decir que las transiciones de los valores de salida se producen durante los flancos activos de las señales de reloj.

Su circuito es:

Imagen 09. Elaboración propia

 

el símbolo es:

Imagen 10. Elaboración propia

 

Su tabla de estados sería:

Y su función lógica:

Cronograma de un biestable J-K síncrono por flanco de subida.

Imagen 11. Elaboración propia

Es igual que el biestable J-K, de modo que estas dos entradas están puenteadas y forman la entrada T de la báscula, de forma que cuando T toma el valor 0 la salida Q_t+1=Q_t, es decir no cambia.

Cuando la entrada T toma el valor 1, la salida cambia de estado (bascula, de ahí su nombre).

En el caso de que se mantenga la entrada T permanente igual a 1, la báscula T se comporta como un divisor de frecuencia de la señal de reloj entre dos.
Su símbolo es como el de la figura adjunta.

Imagen 12. Elaboración propia

Y su tabla de estado: